怎么测试大模型？大模型测试方法

现在大模型测试，跟传统测试不一样，传统测试有个期待结果。
而大模型测试，只有接近期待的结果。
我们测试大模型，主要是看效果，跟期待结果有多大差距。
之前总听人说，召回率，感觉又不是汽车质量召回。
然后看文章，公式看得我云里雾里。

今天来看一下大模型三个最基础且重要的评估指标：准确率 (Accuracy)、精确率 (Precision) 和召回率 (Recall)。

理解它们的关键在于区分看待预测结果的不同视角。我们先从一个最经典的例子——疾病检测入手。

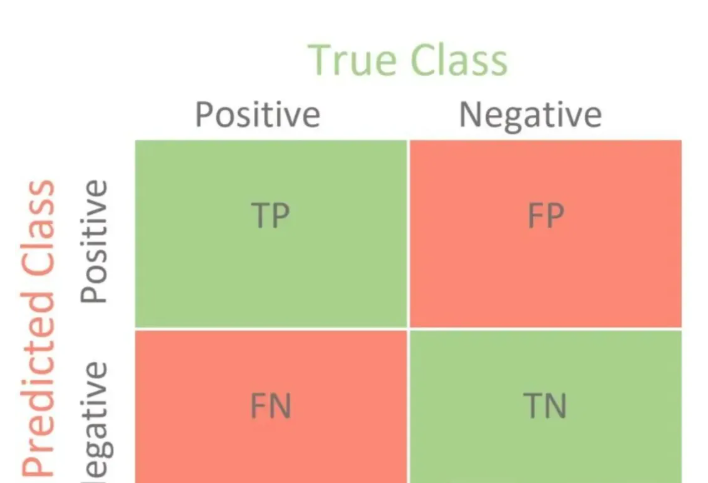
假设我们有一个用于诊断某种疾病的模型，现在我们在一个测试集上运行它，结果可以用一个混淆矩阵 (Confusion Matrix) 来概括：

维度	实际患病 (Positive)	实际健康 (Negative)
预测患病 (Positive)	有病 (True Positive, TP)	误诊 (False Positive, FP)
预测健康 (Negative)	漏诊 (False Negative, FN)	健康 (True Negative, TN)

1. 准确率 (Accuracy)

定义：所有预测正确的样本数占总样本数的比例。
公式：
Accuracy = (TP + TN) / (TP + TN + FP + FN)
理解：顾名思义，它衡量的是模型整体的“正确率”。它是一个非常直观的宏观指标。
优点与局限：
优点：在各类别分布均衡（比如健康人和病人数量差不多）时，它是一个很好的综合性指标。
缺点：在类别不平衡的数据集中，准确率会严重失真。
例子：假设一个城市有1000人，其中只有10人（1%）真正患病。如果一个模型非常“懒”，简单地把所有1000人都预测为健康（相当于漏诊10人），那么它的混淆矩阵是：
TP=0, FP=0, FN=10, TN=990
Accuracy = (0 + 990) / 1000 = 99%
这个99%的准确率看起来非常高，但实际上这个模型连一个病人都没找出来！它是一个完全无用的模型。因此，在类似疾病检测、欺诈识别这种类别极不平衡的场景下，准确率基本没有参考价值，必须看精确率和召回率。

2. 精确率 (Precision) - 又称“查准率”

定义：在所有被模型预测为患病（Positive）的人中，有多少是真正患病的。
公式：
Precision = TP / (TP + FP)
理解：它关注的是预测结果的质量。一个高精确率的模型意味着它非常“精准”，它说某人有病，那么此人很可能真的有病。它惩罚的是“误诊”（False Positive），也就是 “宁纵勿枉” 。
应用场景：当误判成本（False Positive）很高时，我们需要高精确率。
例子：
垃圾邮件检测：如果模型将一封重要工作邮件误判为垃圾邮件（FP），用户可能错过重要信息，这个代价很高。因此我们希望模型非常确定是垃圾邮件时才把它放进垃圾箱，即追求高精确率。
推荐系统：给用户推荐的内容一定要是他可能喜欢的（TP），而不是他不喜欢的（FP）。推荐不相关的内容会损害用户体验。

3. 召回率 (Recall) - 又称“查全率”

定义：在所有真正患病（Actual Positive）的人中，有多少被模型成功预测了出来。
公式：
Recall = TP / (TP + FN)
理解：它关注的是模型发现正例的能力。一个高召回率的模型意味着“宁可错杀一千，不可放过一个”，它能把绝大多数病人都找出来。它惩罚的是“漏检”（False Negative）。
应用场景：当漏检成本（False Negative）很高时，我们需要高召回率。
例子：
疾病检测：如果一个癌症患者被模型误判为健康（FN），他可能因此错过最佳治疗时机，这个代价是致命的。因此我们必须尽可能地把所有潜在病人都找出来复查，即追求高召回率（即使这样会误抓一些健康人FP）。
欺诈交易识别：放过一个欺诈交易（FN）会导致直接的经济损失，因此必须尽可能召回所有可疑交易，交给人工审核。
核心区别与总结

指标	公式	关注点	核心问题	应用场景
准确率 (Accuracy)	(TP+TN)/(TP+TN+FP+FN)	整体正确性	“模型猜对的比例是多少？”	类别平衡的通用任务
精确率 (Precision)	TP/(TP+FP)	预测正例的准确性	“模型说某人有病，这话有多可信？”	误诊成本高（垃圾邮件、推荐）
召回率 (Recall)	TP/(TP+FN)	捕捉正例的全面性	“真正有病的人里，模型找出了多少？”	漏检成本高（疾病、欺诈）

看懂了么？是不是很晕？

举个例子：待检测的潜在新冠病毒携带者有10人阳性(携带)，90人阴性(未携带)，测试仪器对10个阳性样本预测为8阳性，2阴性；对90个阴性样本预测为80阴性，10阳性

本例子中，我们可以计算出(此处要特别注意，TP，TN，FP，FN均指的是个数，不是百分比)：

TP = 8； TN = 80； FP = 10； FN = 2
提出混淆矩阵，是为了计算精确率 precision 和召回率 recall，这两个概念很容易搞混或者难以记忆。但只要记住precision 是针对预测结果的精确度量，而 recall 是针对真实样本的召回度量，就可以很好的理解和记忆了

Precision，针对预测结果而言的，表示预测为正的样本中真实也为正的样本所占比例。即原本为正的样本预测也为正，TP；原本为负的样本预测为正，FP。故 precision = TP / (TP + FP)上面例子的计算结果即为 8/(8+10)=8/18

Recall，针对真实样本而言，表示原本为正的样本有多大比例被预测正确了。即原本为正的样本预测也为正，TP；原本为正的样本预测为负，FN故 recall = TP / (TP + FN)

上面例子的计算结果即为 8/(8+2)=8/10

可见模型的 recall 尚可，但 precision 较低，该模型倾向于将潜在病毒携带者预测为阳性。那么它是一个好模型吗，应该说还不错，但在该场景下，我们其实应该进一步提高其召回率(recall) ，原因是，作为新冠病毒检测，宁可检测为阳性，再次进行检测，也不能放过本身是阳性但没有检测出来的情况。

如果还没懂，我用自己通俗的语言解释一遍，当然不一定准确，但是方便记忆。
精确率，主要是衡量误诊，（把好的说成是坏的）
召回率，主要是衡量漏诊（把坏的说成是好的，有漏网之鱼）
所以这个混淆矩阵，是分两种情况，预测两遍
先从得病的里面预测，在从健康的里面预测（是从预测捞到的角度来看是否正向，不是从健康与否来看）
找到这个规律，就好计算了，就好看模型的效果了。