学习率在梯度下降中的作用？大模型训练的步长设置技巧

Everything can be described as function：世界上任何事物，都可以表示为一种 “输入--->f(x)--->输出” 的函数关系。

先说结论：大语言模型（Large Language Model，LLM）就是在一个多维度的语义空间中，找到这样一个函数f(x)（也就是后面我们要说到的神经网络），使得输入一个语义向量x，预测出对应的语义向量y，作为输出。

1，输入与输出的对应关系

举最简单的例子，在一个二维空间中——一个“xy坐标轴”，我们有一些已知的点，比如（1,4）（2,7）（3,10），那我们可以找到一个对应的函数，y=3x+1，去描述这种关系。

如果未来有人输入了一个新的x，比如x=5，那么我们也可以计算出对应的y的输出等于3*5+1=16

（类比LLM，有人问了一个新问题也就是一个新的x: 天空为什么会是蓝色？那么神经网络的这个函数f(x)，就会计算出对应的答案y，不同的点在于LLM是基于预测概率最大的对应的token，逐字逐句组成的回答。）

2，文字表征成多维向量

人类的想象空间只能到三维（一维x,二维xy,三维xyz）,四维及以上我们无法去画出来以及想象出来，但是我们可以用数学向量来表示，比如一个10维向量，我们表示成【1,2,3,4,5,6,7,8,9,10】。

由于文字与语言无法进行数学运算，所以我们需要将他们用多维的向量去表示，形成一个巨大的语义空间。比如每个字、每个词语，都可以用一个512维度的向量去表示：【6,8,123，...... 342】1*512

这里我们就可以展开想象，有一个512维的巨大语义空间，每个维度都代表一个不同的衡量标准（不准确的比喻，比如一个维度代表心情愉悦数字越大越开心、一个维度代表重量或者长度等），那么语义越相近的词语，他们在这个512维度的向量空间中的距离就越近。比如“乔丹、科比”两个词语作为NBA历史上最伟大的球员之一他俩的“距离”，就会比“李飞飞”（AI人工智能教母）更近一些。

这样表征后，也有助于理解单个词（我们叫token）与单个词之间的关系，也就是理解了句子之间的逻辑规律。有个著名的例子就是，Vking - Vman + Vwoman = Vqueen。

3，多维语义空间里的函数描述

对于比较简单的，给定一组数据，我们来找到一个合适的函数去描述输入x和输出y的情况，我们可以通过各种手段去找到。

但是像语言这种非常复杂的关系，我们只能尽可能的去找到一个相似的函数f`(x)，去尽可能的“贴近”那个目标函数f(x)。

所以，目标从找到一个实际的函数f(x)，变成找到一个函数f'(x)，使得“差值” = f`(x) - f(x)足够小。

这个“差值”的专有名词叫做损失函数。

所以这里我们可以总结一下，大模型的训练，就是在调整成千上亿的参数，找到这个神经网络函数f`(x)，使得“损失函数”尽可能的最小。

4，损失函数L的计算

L = floss(f'(x) - f(x)) = floss(f'(x) - y) = floss(w, (x,y))

这里我们可以看到损失函数L，是关于我们的模拟函数f'(wx)的参数w、以及输入输出x与y的函数。

我们需要确定模拟函数f'(wx)的参数w，使得函数L最小。

根据我们的初中知识，求一个函数的最小值，我们要对它求导。在某点：“导数=0，左导数<0，右导数>0” =>该函数的最小值或局部最小值。

所以对于L=floss((x,y),w)来说，我们可以把它当做是w的函数（固定输入x和输出y），然后求导，然后得到w的值，从而找到我们需要的模拟函数f'(wx）,同时满足L最小。

5，梯度下降

对于前面提的简单例子比如y=3x+1，我们可以直接求导。但是对于大模型神经网络来说，它具有几千亿级别的参数，在目前的科学技术手段直接求导完全不可能。

所以科学家们从“导数”的原理出发，使用一种叫做“梯度下降（Gradient Descent）”的方式求解。

导数表示的是，输入往一个方向变一点点，然后看输出的变化，也是看函数图像“向上或者向下有多陡峭”的数学描述。梯度的意思其实就是高维空间的导数，也就是“向上”变化的方向。既然我们要找导数最小或者等于0的地方，那么我们就朝着梯度的反方向去找就可以了，所以叫做“梯度下降”。

业界最常用的类比就是一个人在复杂的山上去下山，他向某个角度稍微移动一点点，看是向上还是向下了，然后一直试一直试，找到最终的路径。

$$w_{new} = w_{old} - \eta \cdot \frac{dL}{dw}$$

这里的

代表学习率，也就是迈步子的大小。

循环往复：走一步，求一次导；再走一步，再求一次导。直到走到一个坡度几乎为 0 的坑底。

6，求解方式

现实中神经网络的函数可能类似于f(a(b(c(...z(x)))))的套娃形式，以及千亿万亿级别的参数。所以第一我们求每个参数的偏导数，第二我们采取链式法则，从后向前把每一层的导数全部求解（这个就是所谓的“反向传播”）。最后得到一个包含每个参数的导数向量。

链式法则用大白话描述就是，在一个套娃形式的函数中，求里面某个参数的导数，就是分别求解各个函数的导数，然后相乘。

反向传播，其实严格来说，就是链式法则在计算机中的一种高效实现方式，就是从最后开始向前算，这样可以节省计算量。

这里举一个简单的小例子，比如我们有一个三层的神经网络abc，每一层都包含2个参数wi，如下图所示：

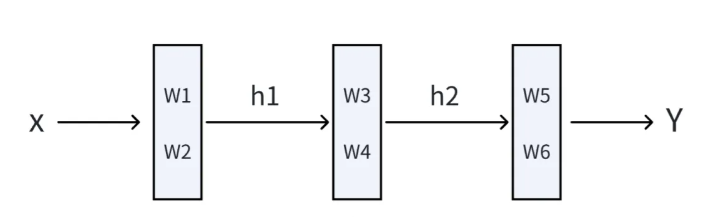
所以这个神经网络我们可以表示成：y=c(b(a(x, w1, w2), w3, w4), w5, w6)，其中w1w2是a函数的参数，w3w4是b函数的参数，w5w6是c函数的参数。为了方便，我们把它隐藏层展开：

h1=a(x, w1, w2)

h2=b(h1, w3, w4)

y=c(h2, w5, w6)

第一步：

求w5的偏导数：∂y/∂w5

注意在这里我们其实已经可以算出w5和w6的偏导数了。以w5为例，我们会把“h2”、“w6”锁定当做已知的参数而不是变量，去计算出一个关于w5的函数。h2在模型训练这个过程中其实已经是“已知的数字”了：因为我们训练模型的过程，是初始化的时候会随机给w1 - w6安排一些初始值，然后我们又有一堆（输入x，输出y）的实际数据，所以我们会先把这些初始值和数据带入进去去计算一个预测值y`，所以第一h2、h1的值我们是知道的，第二这个过程被称为“前向传播”。

所以大家可能会听到模型训练，先进行一次前向传播，然后找预测值和实际值的差距，然后再反向传播算各个参数的梯度，也就是分责任，看看调调某个参数的梯度值，能不能让差距小一点。

求w6的偏导数：∂y/∂w6
我们还需要计算对上一层输入的偏导数∂y/∂h2，因为它是连接上一层的“桥梁”：∂y/∂h2

这里面的tricky在于，我们在计算h2的偏导数的时候，把h2看做是变量，计算完成后，把前向传播过程中计算出来的h2数字，代入进去，从而得到∂y/∂h2的实际结果。

比如，我们的c函数是这样：y = h2^3 + w5 + w6，我们对h2求偏导数，结果应该是3乘以h2的平方，假设我们在前向传播的时候，计算出h2等于6，那么h2的偏导数∂y/∂h=3乘以6的平方，等于108。

第二步：

求w3的偏导数：∂y/∂w3=∂y/∂h2 * ∂h2/∂w3
求w4的偏导数：∂y/∂w4=∂y/∂h2 * ∂h2/∂w4
同样计算h1的偏导数：∂y/∂h1=∂y/∂h2 * ∂h2/∂h1

第三步：

求w1的偏导数：∂y/∂w1=∂y/∂h2 * ∂h2/∂h1 * ∂h1/∂w1 = ∂y/∂h1 * ∂h1/∂w1
求w2的偏导数：∂y/∂w2=∂y/∂h2 * ∂h2/∂h1 * ∂h1/∂w2 = ∂y/∂h1 * ∂h1/∂w2

这样我们就得到了一组w1/w2/w3/w4/w5/w6对y的偏导数组成的向量，然后我们就可以稍微改变一点wi参数，然后看看最终结果的误差有多少，就是类似有成千上万个水龙头开关，技术人员稍微扭转一下开关w1、看看最终结果，然后再扭下开关w2，看看最终结果，直到到达一个技术人员满意的状态为止。

总结，大语言模型并不是在“思考”，而是在一个极高维的语义空间中，通过梯度下降不断调整参数，学会了一个极其复杂的概率函数，从而能够在给定上下文的情况下，预测出最有可能出现的下一个 token。